Write equations of hyperbolas in standard form. Graph hyperbolas centered at the origin. Graph hyperbolas not centered at the origin. Solve applied problems involving hyperbolas. What do paths of comets, supersonic booms, ancient Grecian pillars, and natural draft cooling towers have in common? They can all be modeled by the same type of conic.
Hyperbolas
Yes, that’s correct. At. 0:51. in the segment, the speaker reasoned that the distance from the vertices to the center of the hyperbola is 5 units in the horizontal direction. Since the standard form of the equation of a hyperbola is ( (x – h)^2 / a^2) – ( (y – k)^2 / b^2) = 1 for a hyperbola centered at (h, k), and the hyperbola is centered at

Source Image: bartleby.com
Download Image
From Thinkwell’s College AlgebraChapter 5 Rational Functions and Conics, Subchapter 5.4 Hyperbolas

Source Image: in.pinterest.com
Download Image
SOLVED: 10 -10 Write the standard equation for the hyperbola graphed above To simplify the equation of the ellipse, we letc2 − a2 = b2. x2 a2 + y2 c2 − a2 = 1 So, the equation of a hyperbola centered at the origin in standard form is: x2 a2 − y2 b2 = 1. To graph the hyperbola, it will be helpful to know about the intercepts. We will find the x -intercepts and y -intercepts using the formula.
Source Image: openalgebra.com
Download Image
Write The Standard Equation For The Hyperbola Graphed Above
To simplify the equation of the ellipse, we letc2 − a2 = b2. x2 a2 + y2 c2 − a2 = 1 So, the equation of a hyperbola centered at the origin in standard form is: x2 a2 − y2 b2 = 1. To graph the hyperbola, it will be helpful to know about the intercepts. We will find the x -intercepts and y -intercepts using the formula. The standard form of the equation of a hyperbola with center (0,0) ( 0, 0) and transverse axis on the x -axis is. x2 a2 − y2 b2 =1 x 2 a 2 − y 2 b 2 = 1. where. the length of the transverse axis is 2a 2 a. the coordinates of the vertices are (±a,0) ( ± a, 0) the length of the conjugate axis is 2b 2 b.
OpenAlgebra.com: Free Algebra Study Guide & Video Tutorials: Hyperbolas
Free Hyperbola calculator – Calculate Hyperbola center, axis, foci, vertices, eccentricity and asymptotes step-by-step OpenAlgebra.com: Free Algebra Study Guide & Video Tutorials: Hyperbolas
Source Image: openalgebra.com
Download Image
Equation of Hyperbola Free Hyperbola calculator – Calculate Hyperbola center, axis, foci, vertices, eccentricity and asymptotes step-by-step
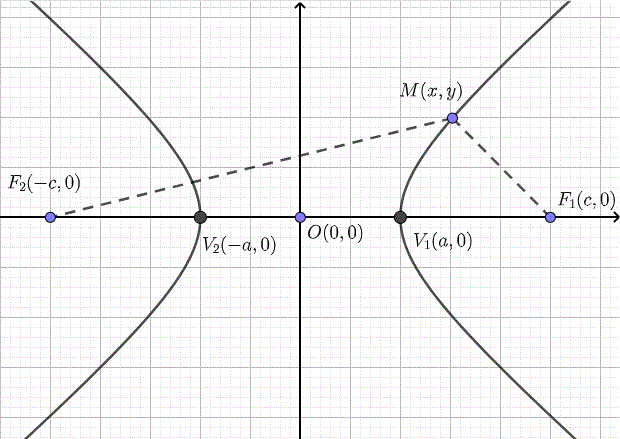
Source Image: analyzemath.com
Download Image
Hyperbolas Write equations of hyperbolas in standard form. Graph hyperbolas centered at the origin. Graph hyperbolas not centered at the origin. Solve applied problems involving hyperbolas. What do paths of comets, supersonic booms, ancient Grecian pillars, and natural draft cooling towers have in common? They can all be modeled by the same type of conic.
Source Image: saylordotorg.github.io
Download Image
SOLVED: 10 -10 Write the standard equation for the hyperbola graphed above From Thinkwell’s College AlgebraChapter 5 Rational Functions and Conics, Subchapter 5.4 Hyperbolas
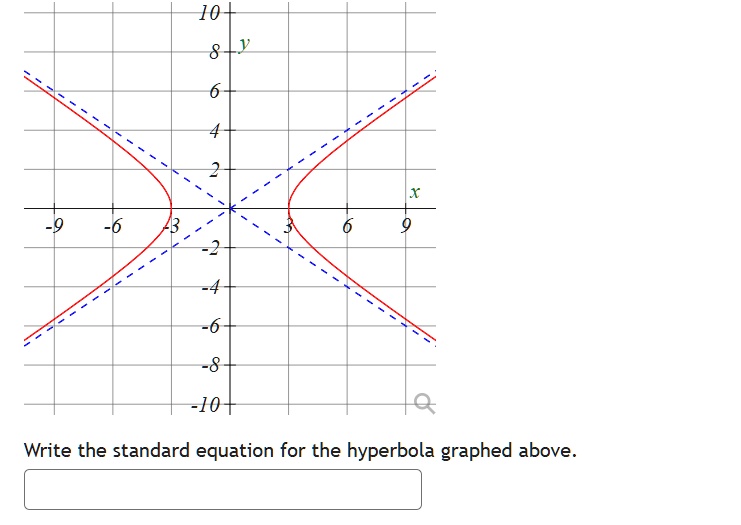
Source Image: numerade.com
Download Image
OpenAlgebra.com: Free Algebra Study Guide & Video Tutorials: Hyperbolas To determine the foci you can use the formula: a 2 + b 2 = c 2 transverse axis: this is the axis on which the two foci are. asymptotes: the two lines that the hyperbolas come closer and closer to touching. The asymptotes are colored red in the graphs below and the equation of the asymptotes is always: Picture
Source Image: openalgebra.com
Download Image
Answered: Write the standard equation for the… | bartleby To simplify the equation of the ellipse, we letc2 − a2 = b2. x2 a2 + y2 c2 − a2 = 1 So, the equation of a hyperbola centered at the origin in standard form is: x2 a2 − y2 b2 = 1. To graph the hyperbola, it will be helpful to know about the intercepts. We will find the x -intercepts and y -intercepts using the formula.

Source Image: bartleby.com
Download Image
Algebra – Hyperbolas The standard form of the equation of a hyperbola with center (0,0) ( 0, 0) and transverse axis on the x -axis is. x2 a2 − y2 b2 =1 x 2 a 2 − y 2 b 2 = 1. where. the length of the transverse axis is 2a 2 a. the coordinates of the vertices are (±a,0) ( ± a, 0) the length of the conjugate axis is 2b 2 b.
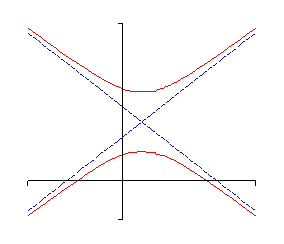
Source Image: tutorial.math.lamar.edu
Download Image
Equation of Hyperbola
Algebra – Hyperbolas Yes, that’s correct. At. 0:51. in the segment, the speaker reasoned that the distance from the vertices to the center of the hyperbola is 5 units in the horizontal direction. Since the standard form of the equation of a hyperbola is ( (x – h)^2 / a^2) – ( (y – k)^2 / b^2) = 1 for a hyperbola centered at (h, k), and the hyperbola is centered at
SOLVED: 10 -10 Write the standard equation for the hyperbola graphed above Answered: Write the standard equation for the… | bartleby To determine the foci you can use the formula: a 2 + b 2 = c 2 transverse axis: this is the axis on which the two foci are. asymptotes: the two lines that the hyperbolas come closer and closer to touching. The asymptotes are colored red in the graphs below and the equation of the asymptotes is always: Picture